Coulomb’s law (Coulomb’s inverse-square law) describes forces between charged particles. It was essential to the development of Electromagnetism.

Background

• Charles Augustin de Coulomb:
  • Born 14 June 1736
    • Angouleme, France
  • Death 23 August 1806 (aged 70)
    • Paris, France
  • French physicist
  • best known for:
    • Coulomb’s Law
      • definition of electrostatic force between particles
    • SI Unit of charge:
      • The coulomb

Other constributors:

• Joseph Priestly
• John Robison
• Henry Cavendish

Coulomb’s Law

For two Charges: \[F = k \frac{q_1 q_2}{r^2}\]

For an Electric Field: \[E = k \frac{Q}{r^2}\]

Line of Charge

Note: variable names might differ

first it can be said that every small charge \(dQ\) is some constant \(\sigma\) times every small length \(dy\),therefore: \[dQ = \sigma dy\]

Additionally the Pythagorean Theorem tells us: \[r = \sqrt{x^2 + y^2}\]

Finally we can also say: \[cos(\theta) = \frac{x}{r}\]

When looking carefully at the setup you can probaly guess that all the \(y\) parts of the equation will end up cancelling out. Therefore only the part of the field that points in the x direction will be significant.

So now we can rewrite the above Electric Field equation: \[E_x = k \frac{\sigma y}{r^2} cos(\theta)\]

Every single one of those infitesimal small charges will have a certain electric Field in the x direction given by: \[dE_x = k \frac{\sigma dy}{x^2+y^2} \frac{x}{r}\]

The total electric field therefore will be: \[\int dE_x = k \sigma x \int_{-a}^b \frac{dy}{(x^2+y^2)^{\frac{3}{2}}}\]

Now with some integral table magic: \[E_x = \frac{k \sigma}{x} \left[ \frac{y}{(x^2+y^2)^{\frac{1}{2}}}\right]_{-a}^b\] \[E_x = \frac{k \sigma}{x} \left[ \frac{b}{(x^2+b^2)^{\frac{1}{2}}} + \frac{a}{(x^2+a^2)^{\frac{1}{2}}} \right]\]

So now as \(a\) and \(b\) approach \(\infty\): \[E_x = \frac{2k \sigma}{x} = \frac{\sigma}{2\pi x \epsilon_0}\]

Ring of Charge

Note: only the ring matters do not worry about the disc just yet.

We are only going to find the field on the axis of the ring. It can easily be seen that the \(z\) and \(y\) parts of the field will cancel out as wherever you are on the \(x\)-axis.

Let \(\theta\) be the angle between the \(z\)-axis and the ring: \(\cos{\theta} = \frac{x}{r}\). Thanks to the Pythagorean Theorem: \(r = \sqrt{x^2+R^2}\). \[E_x = k \frac{Q}{r^2} \cos{\theta} = k \frac{Q x}{r^3} = k \frac{Q x}{(x^2+r^2)^{\frac{3}{2}}}\]

\(Q\) is the total charge here. We did not have to use Calculus here since the distance to all the little charges are the same: \(r\).

We can even take this further and express the total charge in terms of the circumference of the ring: \[E_x = k \frac{\sigma 2\pi R x}{(x^2 + R^2)^{\frac{3}{2}}}\]

Disc of Charge

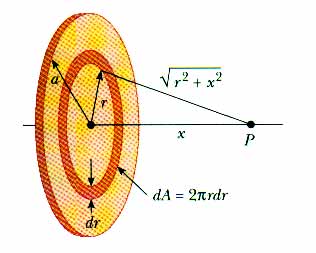
What is a disc? A disc is many rings of different radii.

We only have to rewrite the ring equation in terms of area, since we are now dealing with the area of the disc. Therefore we can reformulate this: \[E_x = k \frac{Q x}{(x^2+r^2)^{\frac{3}{2}}}\]

as this: \[dE_x = k \frac{\sigma (2\pi ) dR x}{(x^2+r^2)^{\frac{3}{2}}}\]

Note: sigma is different here than it was before Evaluating this from the center to the outer parts of the disc gives us:

Now with some integral table magic: \[E_x = k \sigma 2\pi x \left[ 1 - \frac{ x }{\sqrt{x^2+R_{total}^2}} \right]\]

When substituting Colombs’s constant with \(\frac{1}{4\pi \epsilon_0}\) we get: \[E_x = \frac{\sigma x }{2\epsilon_0} \left[ 1 - \frac{ x }{\sqrt{x^2+R_{total}^2}} \right]\]

Sources

• http://en.wikipedia.org/wiki/Coulomb’s_law